• Overview
• Examples of use
• Changes
• Download

ECB - Elliptic Curve Builder - is a generator of ordinary elliptic curves. The curves over the Galois fields GF(P), GF(2^N) and GF(3^N) are built using the so-called complex multiplication method. Even if, for any reason, one does not trust the curves produced with ECB, they remain useful in order to test and/or to tune ECC applications.

Executable for Linux 64-bit (Ubuntu 18.04/x86-64 architecture)
Compiled with Free Pascal 3.0.4 and Lazarus 1.8.2

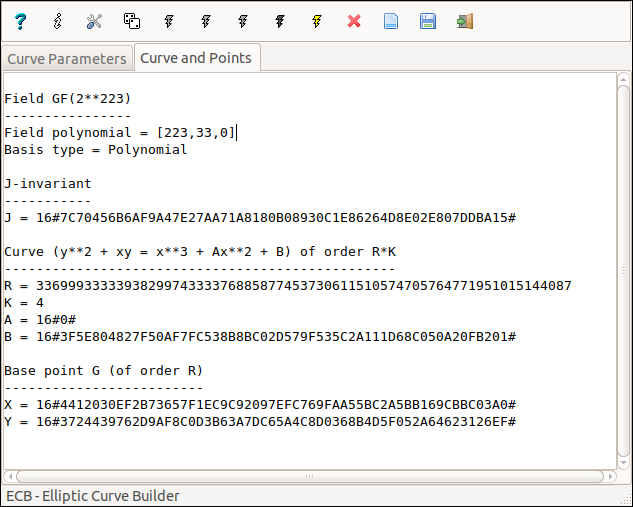Properties of a curve created with ECB

• over GF(P)
  • equation y² = x³ + Ax + B;
  • the order is U = R*K with R prime and K < R;
  • the binary size of the prime modulus P may be any in 30..1536.
    
    
• over GF(2^N)
  • equation y² + xy = x³ + Ax² + B;
  • the order is U = R*K with R prime and K < R;
  • the field degree N may be any in 30..1024;
  • the basis of the field GF(2^N) may be polynomial or normal.
    
    
• over GF(3^N)
  • equation y² = x³ + Ax² + B;
  • the order is U = R*K with R prime and K < R;
  • the field degree N may be any in 20..768;
  • the basis of the field GF(3^N) may be polynomial or normal.
    
    

Here are three examples of use with the three Galois fields:

• Curve and point over GF(P)
• Curve and point over GF(2^N)
• Curve and point over GF(3^N)

• Modified the Setup dialog box.
• Added the Random Seed dialog box.
• Miscellaneous internal improvements.
• Updated the help file.

The ECB software may be used free of charge but it might be a good idea to read the End-User License Agreement before downloading and using it.